Intro to non-negative matrix factorization
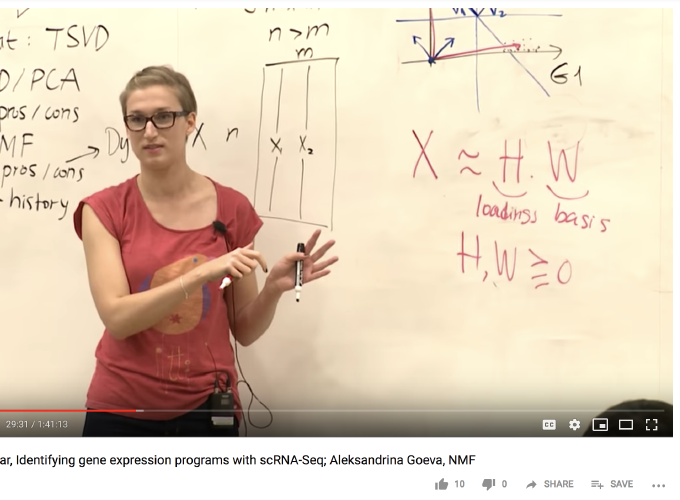
Intro to non-negative matrix factorization
Abstract
Dimensionality reduction is essential for extracting generalizable knowledge from noisy, high-dimensional data. While singular value decomposition (SVD, PCA) is optimal with respect to minimizing data movement, the resulting features are often not interpretable or robust across experiments. Non-negative matrix factorization (NMF) is a powerful alternative that may be applied when the data is non-negative (e.g, counts or concentrations of biological molecules!). In this primer, we will formulate an NMF objective function and optimization algorithm, paying special attention to practical challenges that Dylan will explore in the main talk. We will discuss biomedical applications of NMF, including to spatially-resolved RNA-seq data. And time permitting, we will survey familiar probabilistic models built on NMF, such as the topic models from last week.